Foundations of Computing

Parameterized Approximation Schemes for Clustering with General Norm Objectives

F. Abbassi, S. Banerjee, J. Byrka, P. Chalermsook, A. Gadekar, K. Khodamoradi, D. Marx, R. Sharma, J. Spoerhase

We give a clean and simple approximation scheme for clustering problems. Our algorithm (despite being oblivious to the input structures and objective functions) handles almost all known clustering objectives as well as multiple metric spaces, thus resolving more than 10 clustering problems via a single algorithm.

FOCS’23

---

Functional Lower Bounds in Algebraic Proofs: Symmetry, Lifting, and Barriers

T. Hakoniemi, N. Limaye, I. Tzameret

Ideal Proof System (IPS), introduced by Grochow and Pitassi, is a strong algebraic proof system that is able to simulate most known propositional proof systems. In this work we prove lower new lower bounds for some subsystems of IPS. This includes first explicit lower bounds over finite fields for some fragments of IPS and the strongest to date lower bounds against constant-depth refutations of simple hard instances. Conversely, we show that our techniques cannot yield any non-trivial lower bounds for Boolean instances in any sufficiently strong propositional proof system.

STOC’24 https://doi.org/10.1145/3618260.3649616

---

The Asymptotic Rank Conjecture and the Set Cover Conjecture Are Not Both True

A. Björklund, P. Kaski

We show that Strassen’s asymptotic rank conjecture and the set cover conjecture are inconsistent.

STOC’24 https://doi.org/10.1145/3618260.3649656

---

No distributed quantum advantage for approximate graph coloring

X. Coiteux-Roy, F. d’Amore, R. Gajjala, F. Kuhn, F. Le Gall, H. Lievonen, A. Modanese, M.-O. Renou, G. Schmid, J. Suomela

We give a near-complete characterization of the hardness of graph coloring in distributed settings. We present a classical algorithm and give a near-matching lower bound that holds also for distributed quantum algorithms.

STOC’24 https://arxiv.org/abs/2307.09444

---

Sorting Pattern Avoiding Permutations via 0-1 Matrices forbidding Product Patterns

P. Chalermsook, S. Pettie, S. Yingchareonthawornchai

Improved upper bounds for sorting sequences avoiding a given permutation. The bounds are proved by tight analysis of the density of 0-1 matrices that forbid a certain product pattern. This is a showcase where computer science research questions inspire new directions in extremal combinatorics.

SODA’24

---

A Single-Pass Semi-Streaming Algorithm for (3 + 𝜀)-Approximate Correlation Clustering

M. Cambus, F. Kuhn, E. Lindy, S. Pai, J. Uitto

We consider the correlation clustering problem in the semi-streaming model. We give a single pass algorithm that obtains a (3 + 𝜀)-approximation to minimum disagreement. Our work is the first that works in dynamic streams, where the input can change during the execution of the algorithm.

SODA’24 https://arxiv.org/abs/2205.07593

---

Composable Long-Term Security with Rewinding

R. Berger, B. Broadnax, M. Klooß, J. Mechler, J. Müller-Quade, A. Ottenhues, M. Raiber

Long-Term Security allows to analyze the security of protocols in a setting where all hardness assumptions no longer hold after the protocol execution has finished. In this work, we circumvent existing impossibility results by making use of new techniques, allowing rewinding-based simulation in a way that universal composability is possible. More specifically, we define the notion of security with a rewinding helper and, similar to prior work, provide “robustness theorems” which assert that many protocols remain secure even in the presence of this helper.

TCC’23 https://doi.org/10.1007/978-3-031-48624-1_19 https://eprint.iacr.org/2023/363

---

Chainable Functional Commitments for Unbounded-Depth Circuits

D. Balbás, D. Catalano, D. Fiore, R. W. F. Lai

We introduce a new notion called chainable functional commitments (CFC) and a compiler from CFC for quadratic functions to (C)FC for unbounded-depth circuits. We give a pairing-based construction and a lattice-based construction. These yield the first pairing- and lattice-based FCs and homomorphic signatures for unbounded-depth circuits.

TCC’23 https://doi.org/10.1007/978-3-031-48621-0_13 https://eprint.iacr.org/2022/1365

---

Universally Composable Auditable Surveillance

V. Fetzer, M. Klooß, J. Müller-Quade, M. Raiber, A. Rupp

A balance between privacy and surveillance is often legally imposed, for example by having backdoors which can be used by authorities to disclose a user’s private information (e.g., lawful interception) and which can also be abused. In this work, we develop a building block for auditable surveillance, which divides the system backdoor between multiple parties, and which ensures that, for every surveillance access, an audit trail is left on a public ledger which includes both publicly accessible statistics as well as secret auditing data, which can be used by an auditor to investigate potential abuse of the system.

Asiacrypt’23 https://doi.org/10.1007/978-981-99-8724-5_14 https://eprint.iacr.org/2023/1343

---

Adaptive Massively Parallel Coloring in Sparse Graphs

R. Latypov, Y. Maus, S. Pai, J. Uitto

We study the coloring of everywhere sparse graphs Parametrized by their arboricity. We consider the Adaptive Massively Parallel Computation (AMPC) model that captures distributed communication and cheap remote reads in many data centers. We give an extremely fast, O(1)-round, algorithm that colors the input graph with number of colors polynomial as a function of the arboricity.

PODC’24 https://arxiv.org/abs/2402.13755

---

The Group Access Bounds for Binary Search Trees

P. Chalermsook, M. Gupta, W. Jiamjitrak, A. Pareek, S. Yingchareonthawornchai

We propose a new family of bounds (that generalizes the classical access lemma) for binary search trees. This allows us to unify and strengthen many strong BST bounds that have appeared in the literature under the same framework.

ICALP’24

---

Parameterized Approximation for Clustering in Geometric Spaces

F. Abbassi, S. Banerjee, J. Byrka, P. Chalermsook, A. Gadekar, K. Khodamoradi, D. Marx, R. Sharma, J. Spoerhase

We “complete” the landscape of robust clustering in Euclidean spaces. Moreover, robust clustering (aka socially fair clustering) becomes more tractable in Euclidean spaces, in contrast to the general metric spaces.

ICALP’24

---

Another Hamiltonian Cycle in Bipartite Pfaffian Graphs

A. Björklund, P. Kaski, J. Nederlof

We identify a graph class—the bipartite Pfaffian graphs of minimum degree three—where it is NP-complete to decide whether a given graph in the class is Hamiltonian, but when presented with a Hamiltonian cycle as part of the input, another Hamiltonian cycle can be found in linear time.

ICALP’24 https://arxiv.org/abs/2308.01574

---

Testing Spreading Behavior in Networks with Arbitrary Topologies

A. Modanese, Y. Yoshida

We initiate the study of property testing in dynamic environments with arbitrary topologies. Previous works had only considered the case where the topology was a grid.

ICALP’24 https://arxiv.org/abs/2309.05442

---

Subexponential Parameterized Directed Steiner Network Problems on Planar Graphs: a Complete Classification

E. Galby, S. Kisfaludi-Bak, D. Marx, R. Sharma

In Planar Directed Steiner Network, we are given some input planar digraph G, a set T of terminals, and a demand digraph D on the terminals that is chosen from some fixed class D. The goal is to find a minimum size subgraph of G that satisfies the connectivity requirements among the terminals as defined by D. This is a generalizes several network design problems. We give a complete complexity classification for k=|T| based on the pattern class D.

ICALP’24 https://arxiv.org/pdf/2208.06015

---

Cut paths and their remainder structure, with applications

M. Cairo, S. Khan, R. Rizzi, S. Schmidt, A. I. Tomescu, E. C. Zirondelli

We generalize cut arcs (arcs on all walks between some pair of vertices) to cut paths. The remainder structure of a cut path leads to faster algorithms for some reachability problems from bioinformatics.

STACS’24 https://doi.org/10.4230/LIPIcs.STACS.2023.17

---

Separator Theorem and Algorithms for Planar Hyperbolic Graphs

S. Kisfaludi-Bak, J. Masaříková, E. J. van Leeuwen, B. Walczak, K. Węgrzycki

The hyperbolicity of a graph, informally, measures how close a graph is (metrically) to a tree. In this paper we initiate the study of planar hyperbolic graphs. We prove a strengthening of the planar separator theorem where the separators are geodesic paths or cycles, and derive near-linear fully polynomial time approximation schemes for some prominent graph problems.

SoCG’24 https://arxiv.org/pdf/2310.11283

---

A Quadtree, a Steiner Spanner, and Approximate Nearest Neighbours in Hyperbolic Space

S. Kisfaludi-Bak and G. van Wordragen

We propose a data structure in d-dimensional hyperbolic space that is a natural counterpart to quadtrees in Euclidean spaces. Based on the quadtree, we construct a Steiner spanner, which allows us to solve the Approximate Nearest Neighbor problem in hyperbolic spaces dynamically in an efficient and elegant manner that also outperforms previous algorithms.

SoCG’24 https://arxiv.org/pdf/2305.01356

---

Fine-Grained Complexity of Earth Mover’s Distance under Translation

K. Bringmann, F. Staals, K. Wegrzycki, G. van Wordragen

The Earth Mover’s Distance of two point sets isthe minimum total edge length of a perfect matching between them, and it is an important measure of distance. In this paper we studied the variant where we minimize the distance under translations of one of the point sets. In the 1-dimensional case we give a quadratic algorithm,a nd prove that it is best possible under the Orthogonal Vectors Hypothesis. In higher dimensions we obtain n^{2d+2} algorithms in the L_1 and L_infinity metrics, and rule out n^{o(d)} algorithms under the Exponential Time Hypothesis.

SoCG’24 https://arxiv.org/abs/2403.04356

---

Complexity of Neural Network Training and ETR: Extensions with Effectively Continuous Functions

T. Hankala, M. Hannula, J. Kontinen, J. Virtema

We show that the training problem for NNs equipped with activation functions f_1,..,f_n is as hard as deciding the existential theory of the reals extended with f_1,…,f_n. For the sigmoid activation, decidability of the training problem turns out to be equivalent with the Tarski’s open problem on the decidability of exponential arithmetic. For the sine function the NN training problem is undecidable.

AAAI’24 https://doi.org/10.1609/aaai.v38i11.29118

---

Noise-Aware Statistical Inference with Differentially Private Synthetic Data

O. Räisä, J. Jälkö, S. Kaski, A. Honkela

We show how to generate differentially private synthetic data that permits valid confidence intervals from downstream analysis.

AISTATS’23

---

Individual Privacy Accounting with Gaussian Differential Privacy

A. Koskela, M. Tobaben, A. Honkela

We derive a tighter individual privacy accounting method allowing computing of individual privacy losses using Gaussian differential privacy.

ICLR’23

---

Faster perfect sampling of Bayesian network structures

J. Harviainen, M. Koivisto

We give an algorithm that runs in expected time O(2.829ⁿ), getting below O(3ⁿ) for the first time. Empirically, we observe speedups of several orders of magnitude over the state of the art.

UAI’24

---

The Shortest Even Cycle Problem Is Tractable

A. Björklund, T. Husfeldt, P. Kaski

Given a directed graph as input, we show how to efficiently find a shortest (directed, simple) cycle on an even number of vertices.

SIAM Journal on Computing https://doi.org/10.1137/22M1538260

---

An ETH-Tight Exact Algorithm For Euclidean TSP

M. de Berg, H. L. Bodlaender, S. Kisfaludi-Bak, S. Kolay

In Euclidean TSP, we are given a set of points in Euclidean space, and the goal is to find the shortest closed curve containing all the points. We settle the complexity of this problem by providing a 2^{O(n^{1-1/d})} algorithm via a new separator theorem, and a matching lower bound of 2^{Ω(n^{1-1/d})} under the Exponential Time Hypothesis.

SIAM Journal on Computing https://doi.org/10.1137/22M1469122

---

On counting propositional logic and Wagner’s hierarchy

M. Antonelli, U. Dal Lago, P. Pistone

We introduce an extension of classical propositional logic with counting quantifiers. Beyond providing a sound and complete proof system, we show that validity problems for this logic can capture counting complexity classes and logically characterize Wagner’s hierarchy.

Theoretical Computer Science https://doi.org/10.1016/j.tcs.2023.113928

Distributed Symmetry Breaking on Power Graphs via Sparsification

Maus, S. Peltonen, J. Uitto  

Ruling sets are a central tool in distributed graph algorithms, in particular, in the strong graph shattering
framework. We provide new tools and efficient algorithms to compute rulings sets.

PODC 2023 (to appear)

Locality in online, dynamic, sequential, and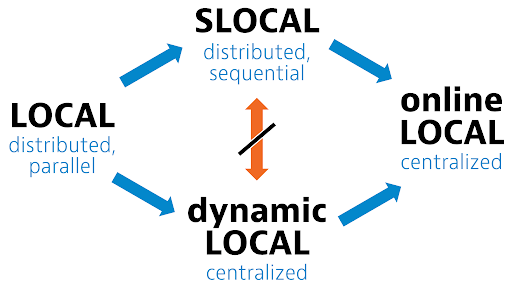 distributed graph algorithms

Akbari, N. Eslami, H. Lievonen, D. Melnyk, J. Särkijärvi, J. Suomela

We give a unifying view of the concept of locality in four settings: distributed algorithms, sequential greedy algorithms, dynamic algorithms,and online algorithms.

ICALP 2023 (to appear)

Fast dynamic programming in trees in the MPC model

Gupta, R. Latypov, Y. Maus, S. Pai, S. Särkkä, J. Studený, J. Suomela, J. Uitto, H. Vahidi   

If we have a tree of diameter D, it is easy to do dynamic programming with parallel algorithms in O(D) rounds:
start with the leaf nodes and propagate information upwards. In this work we show that we can dynamic
programming in the massively parallel computation model exponentially faster, in O(log D) rounds.

SPAA 2023 (to appear)

Optimal Deterministic Massively Parallel Connectivity on Forests

Balliu, R. Latypov, Y. Maus, D. Olivetti, J. Uitto

A parallel algorithm that detects the connected components of an input forests in conditionally optimal time and space.

SODA’23 https://doi.org/10.1137/1.9781611977554.ch99

Improved Pattern-Avoidance Bounds for Greedy BSTs via Matrix Decomposition

Chalermsook, M. Gupta, W. Jiamjitrak, N. O. Acosta, A. Pareek, S. Yingchareonthawornchai

We improve the analysis of Greedy algorithm for online binary search tree, a candidate for dynamic optimality conjecture, for a variety of input sequences. Among various improvements with our new techniques, we also resolve a long-standing post-order traversal conjecture for Greedy.

SODA’23 https://doi.org/10.1137/1.9781611977554.ch22

Efficient Laconic Cryptography from Learning With Errors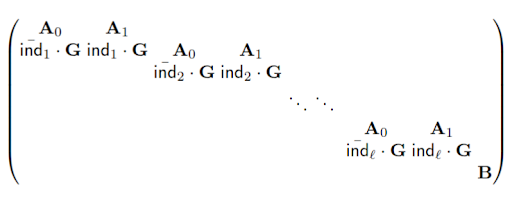

Döttling, D. Kolonelos, R. W. F. Lai, C. Lin, G. Malavolta, A. Rahimi

Laconic cryptography is an emerging paradigm that studies secure two-party computation which is sender-optimised. Although this paradigm has led to tremendous progress in recent years, all existing constructions rely on highly impractical non-black-box cryptographic techniques, making them only of theoretical interest. We provide, for the first time, completely algebraic constructions of laconic primitives which can be proven secure under the standard Learning With Errors (LWE) assumption. We also provide the first proof-of-concept implementation for any laconic primitives, demonstrating that the construction is indeed practical.

EUROCRYPT’23 https://doi.org/10.1007/978-3-031-30620-4_14 https://ia.cr/2023/404

Lattice-based Succinct Arguments from Vanishing Polynomials

Cini, R. W. F. Lai, G. Malavolta

Succinct arguments allow a prover to convince a verifier of the validity of any statement in a language, with minimal communication and verifier’s work. We present some new approaches to constructing efficient lattice-based succinct arguments. Our main technical ingredient is a new commitment scheme based on vanishing polynomials, a notion borrowed from algebraic geometry. A few highlights:

(i) The first recursive folding protocol for linear relations with polylogarithmic verifier runtime. Traditionally, the verifier runtime has been the efficiency bottleneck for such protocols (regardless of the underlying assumptions).

(ii) The first verifiable delay function (VDF) based on lattices, building on a recently introduced sequential relation.

(iii) The first lattice-based linear-time prover succinct argument for NP, in the preprocessing model.

CRYPTO’23

Lattice-Based Timed Cryptography

W. F. Lai, G. Malavolta

Timed cryptography studies primitives that retain their security only for a pre-determined amount of time, such as proofs of sequential work and time-lock puzzles. This feature has proven to be useful in a large number of practical applications, e.g., randomness generation, sealed-bid auctions, or fair multi-party computation. However, the current state of affairs in timed cryptography is unsatisfactory: Virtually all efficient constructions rely on a single sequentiality assumption, namely that repeated squaring in unknown order groups cannot be parallelized. This is a single point of failure in the classical setting and is even false against quantum adversaries.

We put forward a new sequentiality assumption, which essentially says that a repeated application of the standard lattice-based hash function cannot be parallelized. We provide concrete evidence of the validity of this assumption and, to substantiate its usefulness, we show how it enables a new proof of sequential work, with a stronger sequentiality guarantee than prior hash-based schemes.

CRYPTO’23

Publicly Verifiable Zero-Knowledge and Post-Quantum Signatures From VOLE-in-the-Head

Baum, L. Braun, C. Delpech de Saint Guilhem, M. Klooß, E. Orsini, L. Roy, P. Scholl

We present a new method for transforming zero-knowledge protocols in the designated verifier setting into public-coin protocols, which can be made non-interactive and publicly verifiable. Our transformation applies to a large class of ZK protocols based on oblivious transfer. Our resulting ZK protocols have linear proof size, and are simpler, smaller and faster than related approaches based on MPC-in-the-head.

As an application, we present FAEST, a post-quantum signature scheme based on AES. FAEST is the first AES-based signature scheme to be smaller than SPHINCS+, with signature sizes between 5.6 and 6.6kB at the 128-bit security level. Compared with the smallest version of SPHINCS+ (7.9kB), FAEST verification is slower, but the signing times are between 8x and 40x faster.

CRYPTO’23

Sinkless orientation made simple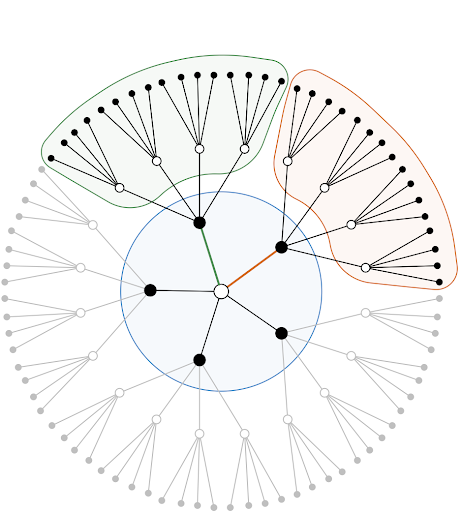

Balliu, J. H. Korhonen, F. Kuhn, H. Lievonen, D. Olivetti, S. Pai, A. Paz, J. Rybicki, S. Schmid,  J. Studený, J. Suomela, J. Uitto

The sinkless orientation problem plays a key role in understanding the foundations of distributed computing. Any deterministic algorithm for sinkless orientation requires Ω(log n) rounds, but all previously known proofs for this result take a complicated detour through randomized algorithms.
We present a new, much simpler proof that gives the result directly for deterministic algorithms.

SOSA’23 https://doi.org/10.1137/1.9781611977585.ch17

On Inference and Learning With Probabilistic Generating Circuits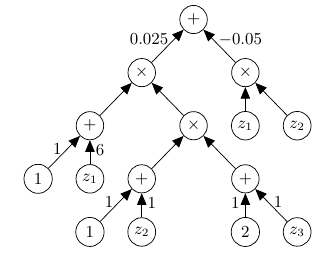

Harviainen, P. R. Vaidyanathan, M. Koivisto

We give significantly faster inference algorithms for probabilistic generating circuits (PGCs). We also show that it is NP-hard to recognize whether a given circuit encodes a probability generating function, hampering efficient learning of PGCs from data.

UAI’23 (to appear)

Research Highlights

The Shortest Even Cycle Problem is Tractable
A. Björklund, T. Husfeldt, P. Kaski.
Given a directed graph as input, we show how to efficiently find a shortest (directed, simple) cycle on an even number of vertices.

STOC’22 https://doi.org/10.1145/3519935.3520030

Deterministic (1+𝜀)-Approximate Maximum matching with poly(1/𝜀) Passes in the Semi-Streaming Model and Beyond

M. Fischer, S. Mitrović, J. Uitto.
In the streaming setting, an input graph is given as a stream of edges and, at any time, the algorithm is allowed to keep a (roughly) linear amount of edges in memory. We give a streaming algorithm that makes a polynomial (in 𝜀)  number of passes over the stream and finds an almost optimal matching.

STOC’22 https://doi.org/10.1145/3519935.3520039

Sparse matrix multiplication in the low-bandwidth model

1. Gupta, J. Hirvonen, J. H. Korhonen, J. Studený, J. Suomela

We study the multiplication of uniformly sparse matrices in a distributed setting. If each row and column has at most d nonzero elements, there is a simple algorithm that solves
the problem in O(d²) communication rounds. We show that it is possible to break this quadratic barrier.

SPAA’22 https://doi.org/10.1145/3490148.3538575

Sparsifying, Shrinking and Splicing for Minimum Path Cover in Parameterized Linear Time

Cáceres, M. Cairo, B. Mumey, R. Rizzi, A. I. Tomescu

The minimum path cover problem asks for a minimum-size set of paths covering all nodes of a directed acyclic graph. It has various applications in scheduling, distributed computing, databases, bioinformatics. We prove that the problem can be solved parameterized-linear time, namely in time O(k3n + m), where k is
the size of such set of paths, and n and m are the number of nodes and arcs of the graph, respectively.

SODA’22 https://doi.org/10.1137/1.9781611977073.18

Online search for a hyperplane in high-dimensional Euclidean space

Antoniadis, R. Hoeksma, S. Kisfaludi-Bak, K. Schewior

We consider the online search problem in which a server starting at the origin of a d-dimensional Euclidean space has to find an arbitrary hyperplane. The best-possible competitive ratio and the length of the shortest curve from which each point on the d-dimensional unit sphere can be seen are within a constant
factor of each other. We show that this length is in Ω(d) ∩ O(d3/2).

Inform. Process. Lett. (2022)
https://doi.org/10.1016/j.ipl.2022.106262

Towards Sub-Quadratic Diameter Computation in Geometric Intersection Graphs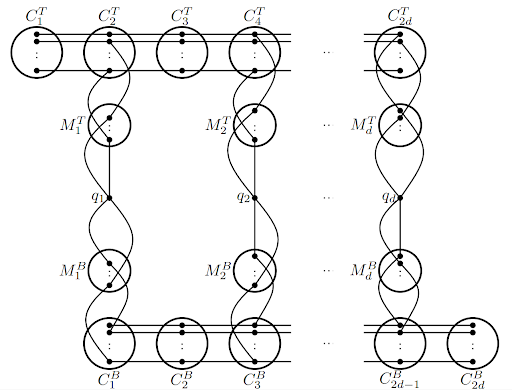

Bringmann, S. Kisfaludi-Bak, M. Künnemann, A. Nusser, Z. Parsaeian

We initiate the study of diameter computation in geometric intersection graphs from the fine-grained complexity perspective. In this work we (conditionally) rule out sub-quadratic algorithms in several classes of intersection graphs, i.e., algorithms of running time O(n2-δ) for some
δ > 0. We show that the hardness of approximation may also depend on dimensionality: for axis-parallel unit hypercubes in ℝ12, distinguishing between diameter 2 and 3 needs quadratic time (ruling out (3/2 – ε)-approximations), whereas for axis-parallel unit squares, we give an algorithm that distinguishes between diameter 2 and 3 in near-linear time. Note that many of our lower bounds match the best known algorithms up to sub-polynomial factors.

SoCG’22 https://doi.org/10.1016/j.ipl.2022.106262

Lattice-Based SNARKs: Publicly Verifiable, Preprocessing, and Recursively Composable

R. Albrecht, V. Cini, R. W. F. Lai, G. Malavolta, S. A. K. Thyagarajan

A succinct non-interactive argument of knowledge (SNARK) allows a prover to produce a short proof that certifies the veracity of a certain NP-statement. We propose the first lattice-based SNARK that simultaneously satisfies many desirable properties: It (i) is tentatively post-quantum secure, (ii) is publicly-verifiable, (iii) has a logarithmic-time verifier and (iv) has a purely algebraic structure making it amenable to efficient recursive
composition. Our construction stems from a general technical toolkit that bridges pairing-based and lattice-based cryptography.

CRYPTO’22 https://doi.org/10.1007/978-3-031-15979-4_4 https://ia.cr/2022/941

Security Analysis of the MLS Key Derivation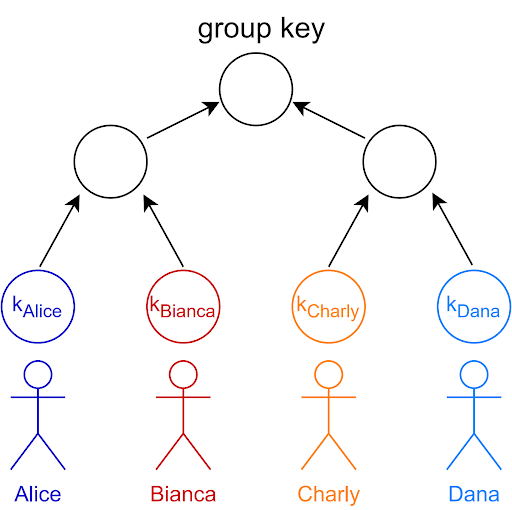

Brzuska, E. Cornelissen, K. Kohbrok

Analysis of the tree-based key derivations in the new cryptographic group messaging protocol MLS.

Security & Privacy 2022

https://doi.org/10.1109/SP46214.2022.9833678

Suggested protocol modifications were integrated into the IETF standard.

https://github.com/mlswg/mls-protocol/pull/453

On Building Fine-Grained One-Way Functions from Strong Average-Case Hardness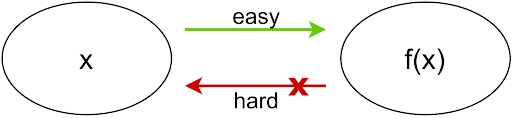

Brzuska, G. Couteau

We show that building one-way functions from average-case hardness is impossible in a black-box way even when assuming self-amplifying, exponential average-case hardness and when trying to build a one-way function with polynomial security gap.

EUROCRYPT’22
https://doi.org/10.1007/978-3-031-07085-3\_20

Trustworthy Monte Carlo

Harviainen, P. Kaski, M. Koivisto

We extend Monte Carlo estimators so that the correctness of  outsourced computations can be verified.

NeurIPS’22 (to appear, https://openreview.net/forum?id=jglXPY6gH-1)

Deterministic Small Vertex Connectivity in Almost Linear Time

Saranurak, S. Yingchareonthawornchai

We study vertex connectivity through the lens of derandomization. We provide an almost linear time algorithm for small connectivity using expanders and vertex cut sparsifiers, breaking the
quadratic-time barrier.

FOCS’22 https://doi.org/10.1109/FOCS54457.2022.00080

Lower Bounds for Maximal Matchings and Maximal Independent Sets

A. Balliu, S. Brandt, J. Hirvonen, D. Olivetti, M. Rabie, J. Suomela.

There is a simple distributed algorithm for finding a maximal matching in a bipartite graph: nodes on one side send proposals one by one to their neighbors, and nodes on the other side accept the first proposal they get. In a graph of maximum degree Δ this takes O(Δ) rounds. We show that this is optimal: any distributed algorithm requires Ω(Δ) rounds in large networks.

J. ACM (2021) https://doi.org/10.1145/3461458

Approximating the Permanent with Deep Rejection Sampling

J. Harviainen, A. Röyskö, M. Koivisto.

Our deep rejection sampling method yields the fastest known practical approximation scheme for the permanent of nonnegative matrices. The key idea is to compute tighter upper bounds for the permanent by exact evaluation of the permanent of appropriate rectangular matrices.

NeurIPS’21 [link to online proceedings]

Exponential suppression of bit or phase errors with 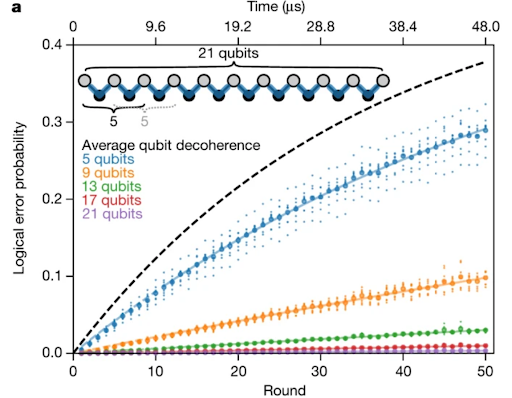cyclic error correction

Chen, K.J. Satzinger, …., A. Paler, …, A. Megrant, J. Kelly

We perform error detection with a small logical qubit and show that the results agree with numerical simulations.
These experimental demonstrations provide a foundation for building a scalable fault-tolerant quantum computer with superconducting  qubits.

Nature 595 (2021)
https://www.nature.com/articles/s41586-021-03588-y